3DMatics

Here we look at the Pocket algorithm that addresses an important practical issue of PLA stability and the absence of convergence for non-separable training dataset.

Generating Non-Separable Training Datasets

A minor modification for the code from the previous post on generation of artificial linearly separable datasets allows to generate “almost” separable data, i.e. data where number of data points that violate linear separability can be controlled and the max violation distance from the “true” decision boundary is a parameter. The code below uses function value_on instead of class_of (see Classifier python code in one of the previous posts). That allows to pick data point class randomly within the boundary of specified “width” around classifier’s decision boundary. (The width here is in quotes because the classifier linear function vect_w is not normalized.)

def nearly_separable_2d(seed, n_points, classifier, boundary_width):
    '''Generates n_points which are not linearly separable with
    a controlled degree of inseparability (in 2d). The classifier has
    to be able to return floating point value of the underlying linear
    function. 

    :params seed: sets random seed for the random generator,

    :params n_points: number of points to generate,

    :params classifier: a linear function returning floating point
        for each point in 2d;

    :params boundary_width: instead of using comparison of 
        classifier.value_on(data point) with 0 we will compare 
        it with a random number in the range [-boundary_width, boundary_width]
        to assign the class +1 or -1 to a data point.
    '''
    np.random.seed(seed)

    dim_x = 2
    data_dim = dim_x + 1 + 1  # leading 1 and class value
    data = np.ones(data_dim * n_points).reshape(n_points, data_dim)

    # fill in random values
    data[:, 1] = -1 + 2*np.random.rand(n_points)
    data[:, 2] = -1 + 2*np.random.rand(n_points)
    # in the vicinity of boundary generate random number
    # to decide on the class of the data point: 
    rand_boundary = -1 + 2*np.random.rand(n_points)
    rand_boundary *= boundary_width
    
    # TODO: use numpy way of applying a function to rows
    for idx in range(n_points):
        curr_val = classifier.value_on(data[idx])
        data[idx,-1] = 1 if rand_boundary[idx] < curr_val else -1

    return data

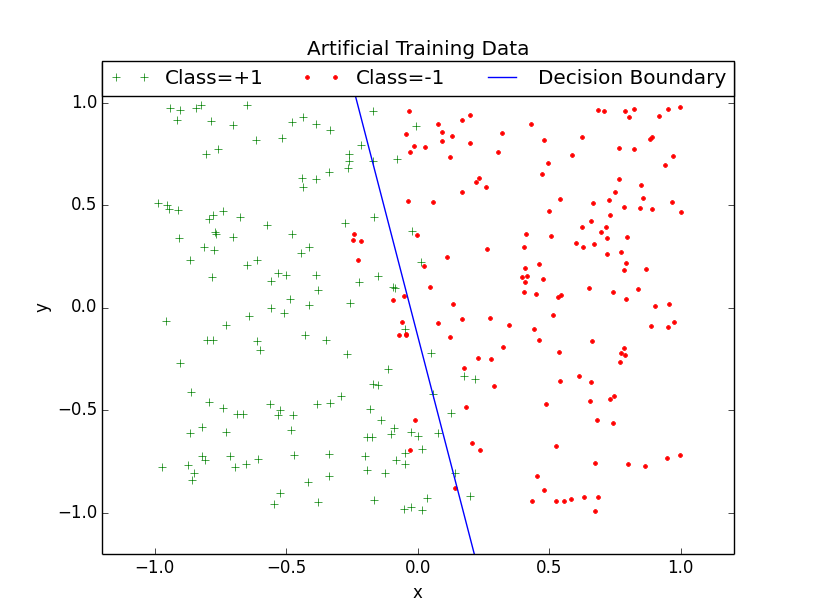
Below is a plot of 300 training points generated using the code above. Note that the separability violators are concentrated around the decision line of the classifier used to generate data.

Pocket PLA

Modifications done to the PLA to support the Pocket algorithm are obvious and there is no need to present them. Now the PLA should also check for both – convergence criteria and the max iteration limit to terminate.

Animations

The following two animations show behavior of the Pocket PLA on artificial datasets with non-separable data generated by function nearly_separable_2d above. The max iteration number was set to 100. Both animations show that updates on later steps are mostly happening on the datapoints that violate linear separability.  Click on the thumbnail to see the gif animation.

Pocket PLA. Dataset 1.

Pocket PLA. Dataset 2.

References

[1] Yaser S. Abu-Mostafa, Malik Magdon-Ismail, Hsuan-Tien Lin. “Learning From Data” AMLBook, 213 pages, 2012.
[2] Wikipedia (http://en.wikipedia.org/wiki/Perceptron)