3DMatics

Adaptive linear neuron (or element) aka Adaline can be viewed as a variation of PLA with update scaled by the mismatch magnitude. While not the universally best choice for the classifier learning algorithm, Adaline can be viewed as an improvement over the original PLA.

Notation and PLA error measure

Training vectors are elements of and they are classified using two classes so that the the training set is the set of pairs . Lets define a linear functional on space where is dot product, which by definition is: (). The class of  is defined as if and otherwise. An error measure on the training set for a given can be defined in many ways. The PLA can be treated as if it measures error as the number of misclassified samples. Using different measures leads to modified update rules that still resemble PLA update rule but may give an advantage.

The 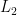Error

Lets define error measure on the training dataset as follows.

(1)

Note that the does not care about mapping but uses the value of on the training vector directly. Minimizing (1) would be equivalent to fitting linear regression solution to classification problem. While this may not be the best approach in general, it may still lead to a reasonable update rules that would make PLA more efficient.

An iterative solution for linear regression would require to compute gradient of (1) with respect to  and update it on every step using that gradient scaled by some learning rate . The gradient calculation is straightforward:

(2) = =

where is coordinate index in . The coordinate-wise formula (2) is equivalent to the following one in more compact vector notation:

(3)

The general gradient descent update with learning rate is:

(4)

If we focus on a single misclassified sample (i.e. single term in the summation (3)) instead of the full batch update (4), we will get an update rule:

(5)

This is a variation of Adaline (from Adaptive Linear Element or Neuron) that can be viewed as a variant of PLA (see post). The main differences are the introduction of learning rate and the use of the current mismatch of the desired output from the target class which amplifies updates more for samples with larger deviation from the target.

Adaline Python code

An update to our running PLA code example (again see this post) to support the Adaline modification is nearly trivial:

class AdalineCLA(PLA):
    '''
    Adaptive linear element Classifier Learning Algorithm (CLA).
    The algorithm approximately minimizes square error of classification.
    '''
    def __init__(self, training_data, learning_rate=1):
        '''In addition to training data constructor takes learning
        rate parameter, a multiplier that replaces 1 in the PLA.'''
        self.n_points = training_data.shape[0]
        self.learning_rate = learning_rate
        self.curr_values = np.ones(self.n_points)
        PLA.__init__(self, training_data)

    def update_error_measure(self):
        '''In addition to PLA, updates and stores the value of linear functional 
        used in the classifier.'''
        self.classifier.values_on(self.data, self.curr_values)
        PLA.update_error_measure(self)

    def update_classifier(self):
        '''Updates classifier's decision vector.'''
        delta_vect = self.data[self.update_idx, :-1]
        curr_value = self.curr_values[self.update_idx]
        target_class = self.data[self.update_idx, -1]
        multiplier = 2*abs(target_class - curr_value)
        self.classifier.vect_w[:-1] += target_class * \
                                       multiplier * \
                                       self.learning_rate * \
                                       delta_vect

The selection rule for the update index remains the same. We used abs function to emphasize the source of the actual sign of the update: it comes form the the target class just like in PLA. Making batch version of Adaline (class BatchAdalineCLA sub-classed from class AdalineCLA) is also straightforward:

    def update_classifier(self):
        '''Batch version: updates classifier's decision vector by
        accumulating error from all misclassified samples.'''
        for idx in self.misclassified:
            delta_vect = self.data[idx, :-1]
            curr_value = self.curr_values[self.update_idx]
            target_class = self.data[self.update_idx, -1]
            multiplier = 2*abs(target_class - curr_value)
            self.classifier.vect_w[:-1] += target_class * \
                                       multiplier * \
                                       self.learning_rate * \
                                       delta_vect

We leave out obvious changes to super-classes needed to keep the list of misclassified samples (or compute it dynamically). In the batch version the contribution from all misclassified samples is accumulated during single epoch update. This affects sensible choice of learning rate: it has to be smaller than that one for by-sample Adaline. An obvious rule of thumb is to make the learning rate proportional to 1/n_points. Proper selection of learning rate may influence the convergence significantly with trade off between convergence speed and proximity of the result to the optimal (in sense) solution. We will leave comparison of various flavors of PLA to one of the next posts. With a good learning rate selection batch Adaline can give significant speed-up over other variations of PLA. The following example converged only in 10 epochs, with is much faster than 38 epochs for the same data in one of the previous posts (second example). Click on the thumbnail to see gif animation:

Batch Adaline

References

For short high level description see Wikipedia [1]. The book [2] discusses Adaline as an exercise and treats it as a variation of PLA. This is the approach we followed while implementing Adaline in Python.

[1] http://en.wikipedia.org/wiki/ADALINE
[2] Yaser S. Abu-Mostafa, Malik Magdon-Ismail, Hsuan-Tien Lin. “Learning From Data” AMLBook, 213 pages, 2012.